Selle ajaveebi kood koos andmekogumiga on saadaval järgmisel lingil https: // github.com / shekharpandey89 / k-tähendab
K-Means klastramine on järelevalveta masinõppe algoritm. Kui võrrelda K-Means järelevalveta klastrialgoritmi jälgitava algoritmiga, ei ole vaja mudelit koolitada sildistatud andmetega. K-Means algoritmi kasutatakse erinevate objektide atribuutide või tunnuste alusel klassifitseerimiseks või rühmitamiseks K arvu rühmadesse. Siin on K täisarv. K-Means arvutab kauguse (kasutades kauguse valemit) ja seejärel leiab andmete klassifitseerimiseks minimaalse kauguse andmepunktide ja tsentroidklastri vahel.
Mõistame K-tähiseid, kasutades väikest näidet, kasutades 4 objekti, ja igal objektil on 2 atribuuti.
| ObjectsName | Atribuut_X | Atribuut_Y |
|---|---|---|
| M1 | 1 | 1 |
| M2 | 2 | 1 |
| M3 | 4 | 3 |
| M4 | 5 | 4 |
K-vahend numbrilise näite lahendamiseks:
Ülaltoodud arvulise probleemi lahendamiseks K-Means'i kaudu peame järgima järgmisi samme:
K-Means algoritm on väga lihtne. Kõigepealt peame valima suvalise arvu K ja valima seejärel klastrite tsentriidid või keskpunkti. Tsentriidide valimiseks saame initsialiseerimiseks valida suvalise arvu objekte (sõltub K väärtusest).
K-Means algoritmi põhisammud on järgmised:
- Jätkab töötamist seni, kuni ükski objekt ei liigu oma tsentriididest (stabiilne).
- Mõned tsentriidid valime kõigepealt juhuslikult.
- Seejärel määrame iga objekti ja tsentriidide vahelise kauguse.
- Objektide rühmitamine minimaalse kauguse põhjal.
Niisiis, igal objektil on kaks punkti X ja Y ning need kujutavad graafiku ruumis järgmist:
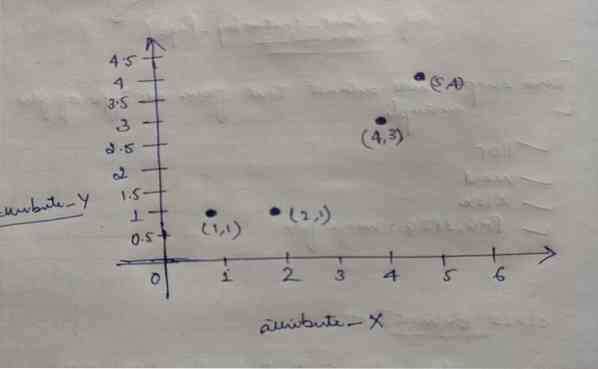
Nii et valime oma ülaltoodud probleemi lahendamiseks algselt K = 2 väärtuse juhuslikult.
1. samm: Esialgu valime kaks esimest objekti (1, 1) ja (2, 1) oma tsentriidideks. Allpool olev graafik näitab sama. Nimetame neid kesknõudeid C1 (1, 1) ja C2 (2,1). Siinkohal võime öelda, et C1 on rühm_1 ja C2 on rühm_2.
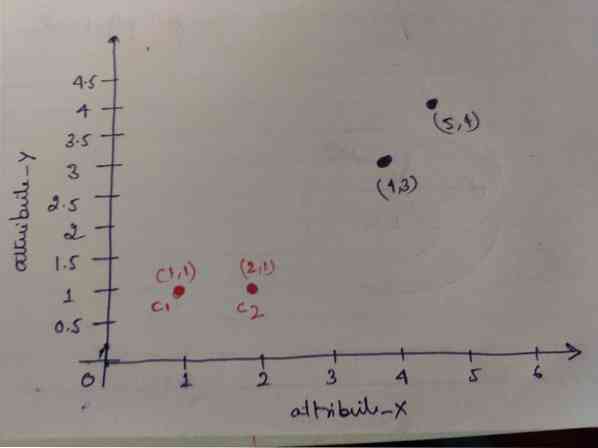
2. samm: Nüüd arvutame iga objekti andmepunkti keskpunktideks, kasutades Eukleidese kauguse valemit.
Vahemaa arvutamiseks kasutame järgmist valemit.

Arvutame kauguse objektidest tsentriididesse, nagu on näidatud alloleval pildil.

Niisiis, arvutasime iga objekti andmepunkti kauguse ülaltoodud kaugusmeetodi abil, lõpuks saime kaugusmaatriksi, nagu allpool esitatud:
DM_0 =
| 0 | 1 | 3.61 | 5 | C1 = (1,1) klaster1 | grupp_1 |
| 1 | 0 | 2.83 | 4.24 | C2 = (2,1) klaster2 | rühm_2 |
| A | B | C | D | |
|---|---|---|---|---|
| 1 | 2 | 4 | 5 | X |
| 1 | 1 | 3 | 4 | Y |
Nüüd arvutasime iga objekti kauguse väärtuse iga tsentroidi jaoks. Näiteks on objektipunktide (1,1) kaugus väärtusest c1 0 ja c2 1.
Kuna ülaltoodud kaugusmaatriksist saame teada, et objektil (1, 1) on klastri1 (c1) kaugus 0 ja klastrini2 (c2) 1. Niisiis on objekt üks klastri1 lähedal.
Samamoodi on objekti (4, 3) kontrollimisel kaugus klastrini 1 3.61 ja klastrisse 2 on 2.83. Niisiis, objekt (4, 3) nihkub klastris2.
Samamoodi, kui kontrollite objekti (2, 1), on kaugus klastrini1 1 ja klastrini2 0. Niisiis nihkub see objekt klastriks2.
Nüüd, vastavalt nende kauguse väärtusele, rühmitame punktid (objektide rühmitamine).
G_0 =
| A | B | C | D | |
|---|---|---|---|---|
| 1 | 0 | 0 | 0 | grupp_1 |
| 0 | 1 | 1 | 1 | rühm_2 |
Nüüd, vastavalt nende kauguse väärtusele, rühmitame punktid (objektide rühmitamine).
Ja lõpuks näeb graafik välja pärast klastrite tegemist allpool olevat (G_0).
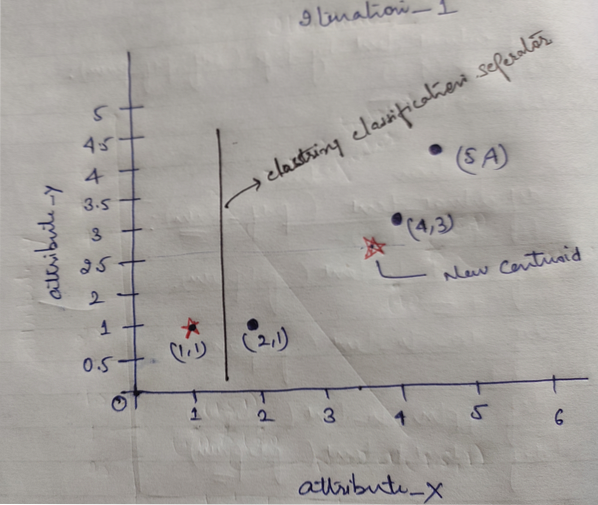
Kordus_1: Nüüd arvutame uued tsentriidid, kui algsed rühmad muutuvad vahemaa valemi tõttu, nagu on näidatud G_0-s. Seega on grupil_1 ainult üks objekt, seega on selle väärtus endiselt c1 (1,1), kuid grupil_2 on 3 objekti, seega on selle uus tsentroidväärtus 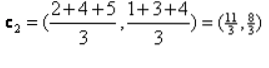
Niisiis, uued c1 (1,1) ja c2 (3.66, 2.66)
Nüüd peame jälle arvutama kogu kauguse uutest keskosadest, nagu me varem arvutasime.
DM_1 =
| 0 | 1 | 3.61 | 5 | C1 = (1,1) klaster1 | grupp_1 |
| 3.14 | 2.36 | 0.47 | 1.89 | C2 = (3.66,2.66) klaster2 | rühm_2 |
| A | B | C | D | |
|---|---|---|---|---|
| 1 | 2 | 4 | 5 | X |
| 1 | 1 | 3 | 4 | Y |
Iteratsioon_1 (objektide klasterdamine): Nüüd rühmitame uue kaugusmaatriksi (DM_1) arvutamise nimel selle vastavalt sellele. Niisiis, nihutame objekti M2 grupist_2 gruppi_1 kui minimaalse kauguse reeglit tsentriidideni ja ülejäänud objekt on sama. Nii et uus klasterdamine toimub allpool.
G_1 =
| A | B | C | D | |
|---|---|---|---|---|
| 1 | 1 | 0 | 0 | grupp_1 |
| 0 | 0 | 1 | 1 | rühm_2 |
Nüüd peame uuesti arvutama uued tsentriidid, kuna mõlemal objektil on kaks väärtust.
Niisiis, uued tsentriidid saavad olema 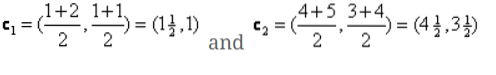
Niisiis, pärast uute tsentriidide saamist näeb klaster välja järgmine:
c1 = (1.5, 1)
c2 = (4.5, 3.5)
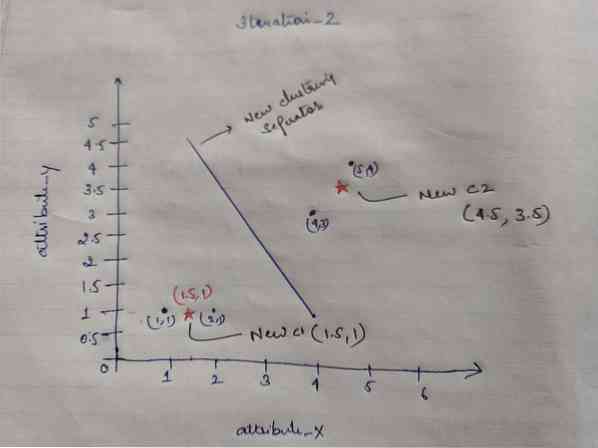
Kordus_2: Kordame sammu, kus arvutame iga objekti uue kauguse uutest arvutatud tsentriididest. Niisiis, pärast arvutust saame iteratsiooni jaoks järgmise kaugusmaatriksi.
DM_2 =
| 0.5 | 0.5 | 3.20 | 4.61 | C1 = (1.5, 1) klaster1 | grupp_1 |
| 4.30 | 3.54 | 0.71 | 0.71 | C2 = (4.5, 3.5) klaster2 | rühm_2 |
A B C D
| A | B | C | D | |
|---|---|---|---|---|
| 1 | 2 | 4 | 5 | X |
| 1 | 1 | 3 | 4 | Y |
Jällegi teeme klastrite määramise miinimumkauguse põhjal nagu varemgi. Nii et pärast selle tegemist saime klastrite maatriksi, mis on sama mis G_1.
G_2 =
| A | B | C | D | |
|---|---|---|---|---|
| 1 | 1 | 0 | 0 | grupp_1 |
| 0 | 0 | 1 | 1 | rühm_2 |
Nagu siin, G_2 == G_1, nii et edasist kordamist pole vaja ja võime siin peatuda.
K-tähendab rakendust Pythoni abil:
Nüüd juurutame Pythonis K-tähendusliku algoritmi. K-keskmiste rakendamiseks kasutame kuulsat Irise andmekogumit, mis on avatud lähtekoodiga. Selles andmekogumis on kolm erinevat klassi. Sellel andmekogul on põhimõtteliselt neli funktsiooni: Hapniku pikkus, tupplehe, kroonlehe pikkus ja kroonlehe laius. Viimases veerus öeldakse selle rea klassi nimi nagu setosa.
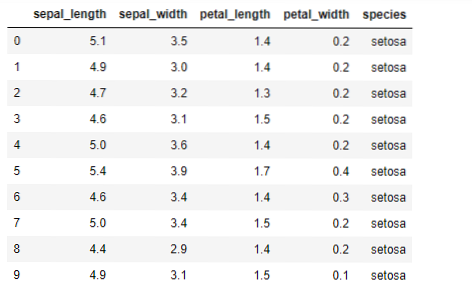
Andmekogum näeb välja järgmine:
Püüton k-tähendab rakendamiseks peame importima vajalikud teegid. Nii et impordime sklearnist Pandad, Numpy, Matplotlib ja ka KMeans.allpool toodud segisti:

Me loeme Iirist.csv-andmekogum, kasutades panda read_csv meetodit, ja kuvab 10 parimat tulemust, kasutades head-meetodit.
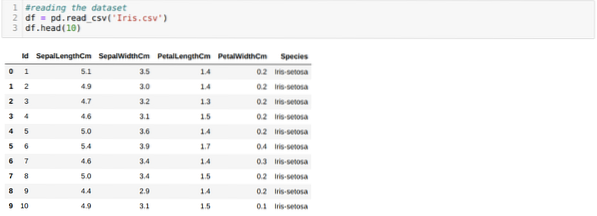
Nüüd loeme ainult neid andmekogumi funktsioone, mida me mudeli koolitamiseks vajame. Niisiis loeme kõiki andmekogumite nelja funktsiooni (tupplehe, tupe laius, kroonlehe pikkus, kroonlehe laius). Selleks viisime neli indeksi väärtust [0, 1, 2, 3] panda andmeraami iloc funktsiooni (df), nagu allpool näidatud:
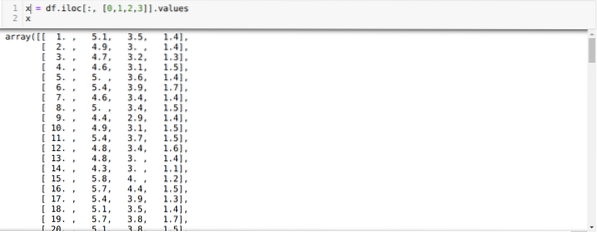
Nüüd valime klastrite arvu juhuslikult (K = 5). Loome K-klassi klassi objekti ja seejärel sobitame oma x andmekogumi koolituse ja prognoosimise jaoks, nagu allpool näidatud:
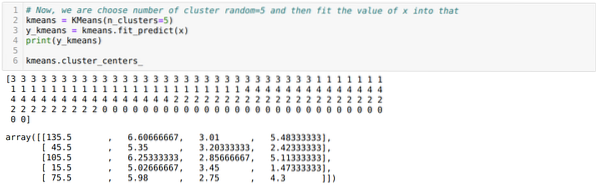
Nüüd visualiseerime oma mudeli juhusliku K = 5 väärtusega. Näeme selgelt viit klastrit, kuid tundub, et see pole täpne, nagu allpool näidatud.
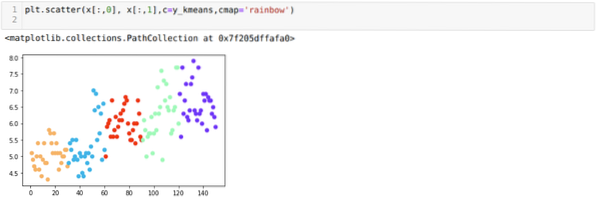
Seega on meie järgmine samm teada saada, kas klastrite arv oli täpne või mitte. Ja selleks kasutame küünarnuki meetodit. Konkreetse andmekogumi klastri optimaalse arvu väljaselgitamiseks kasutatakse küünarnuki meetodit. Seda meetodit kasutatakse selleks, et teada saada, kas k = 5 väärtus oli õige või mitte, kuna me ei saa klastreid selgeks. Pärast seda läheme järgmisele graafikule, mis näitab, et K = 5 väärtus pole õige, kuna optimaalne väärtus jääb vahemikku 3 või 4.
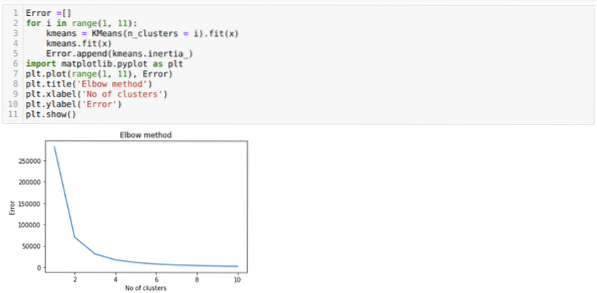
Nüüd käivitame ülaltoodud koodi uuesti klastrite arvuga K = 4, nagu allpool näidatud:
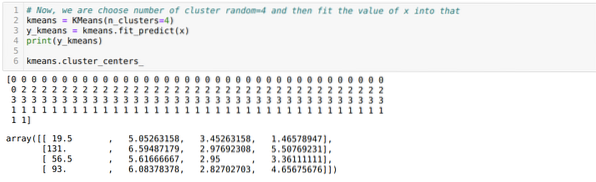
Nüüd visualiseerime ülaltoodud K = 4 uue järgu klastrite. Allpool olev ekraan näitab, et nüüd toimub klasterdamine k-vahendite abil.
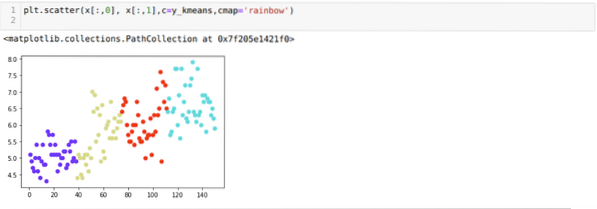
Järeldus
Niisiis, uurisime K-keskmise algoritmi nii arv- kui ka Pythoni koodis. Samuti oleme näinud, kuidas saame teada konkreetse andmekogumi klastrite arvu. Mõnikord ei saa küünarnuki meetod anda õiget klastrite arvu, nii et sel juhul saame valida mitu meetodit.
 Phenquestions
Phenquestions